Understanding Polygons: A Beginner's Guide

Understanding Polygons: A Beginner's Guide

Polygons are fundamental shapes in geometry, each consisting of straight lines that connect to form a closed shape. They can be as simple as a triangle with three sides or as complex as a dodecagon with twelve sides. This article provides a detailed introduction to polygons, offering insights into their properties, types, and real-world applications. Whether you are a student starting out in geometry or a curious learner, understanding polygons is a crucial step in grasping broader mathematical concepts.

1. Defining Polygons

• A polygon is a two-dimensional geometric figure made up of a finite number of straight line segments closing in a loop to form a closed chain or circuit. These line segments are called edges or sides, and the points where two edges meet are the polygon's vertices (or corners).
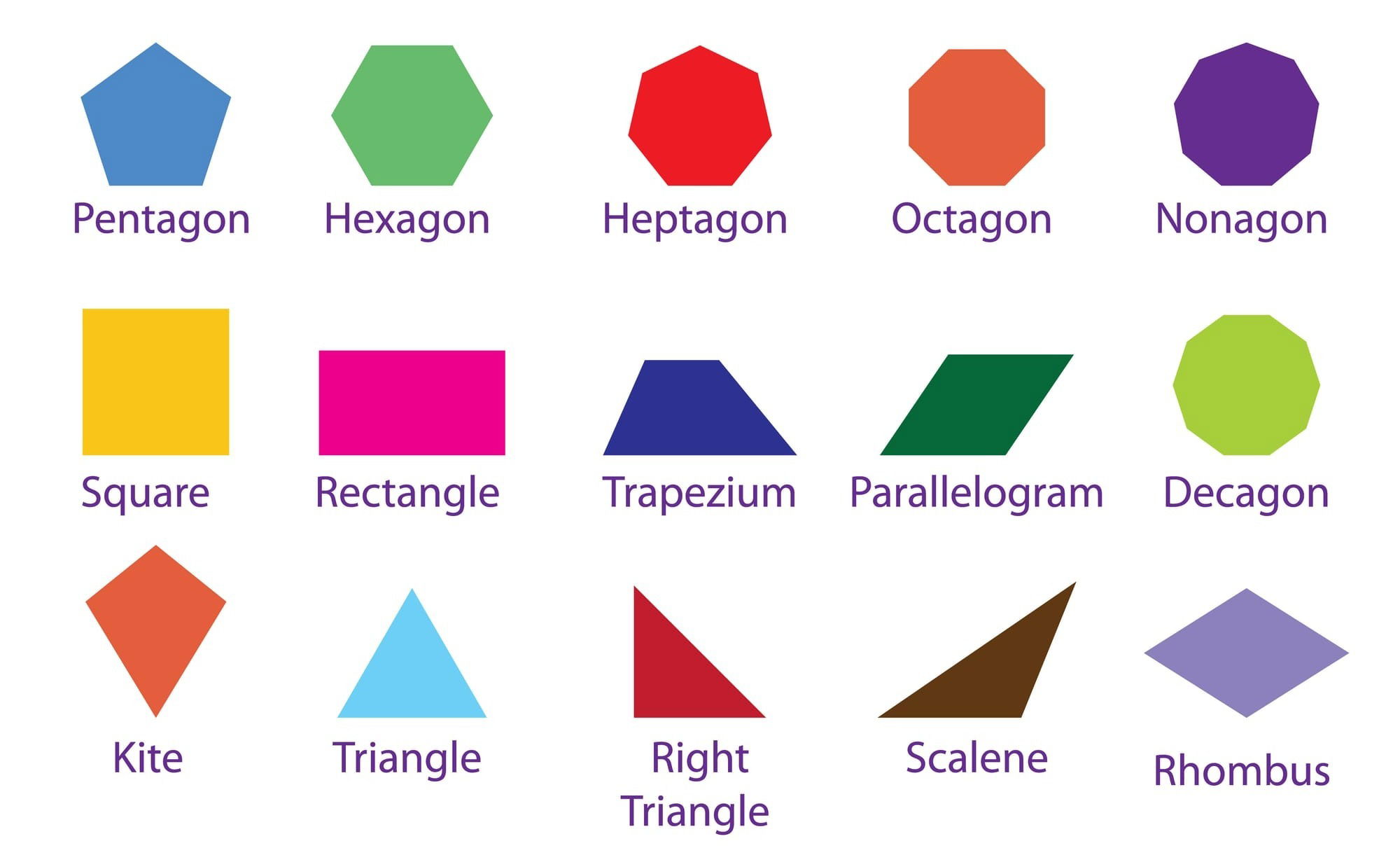
• Polygons are named based on the number of their sides and angles. For example, a three-sided polygon is called a triangle, a four-sided one is a quadrilateral, and so on.
• The interior of the polygon is called its body. Polygons do not have curved sides; if a figure has curves, it is not considered a polygon.

2. Types of Polygons

• Regular vs. Irregular: A regular polygon has all sides and angles equal, like an equilateral triangle or a square. An irregular polygon has sides and angles that are not equal.
• Convex vs. Concave: In convex polygons, all interior angles are less than 180 degrees, and no line segment between any two vertices will pass outside of the polygon. Concave polygons have at least one interior angle greater than 180 degrees, and at least one line segment between vertices passes outside of the polygon.
• Simple vs. Complex: A simple polygon's sides do not intersect, except at their vertices. Complex polygons, which can also be referred to as self-intersecting or crossed polygons, have sides that intersect at points other than the vertices.

3. Polygon Properties

• Sides and Angles: The angles of a polygon are determined by the number of sides it has. For example, a triangle’s angles always add up to 180 degrees, while a quadrilateral’s angles add up to 360 degrees.
• Diagonals: The diagonal of a polygon is a line segment connecting any two non-adjacent vertices. The number of diagonals of a polygon can be calculated using the formula n(n - 3) / 2, where n is the number of sides.
• Perimeter: The perimeter of a polygon is the total length of its sides. For regular polygons, calculating the perimeter involves multiplying the length of one side by the number of sides.
• Area: Calculating the area of a polygon can vary depending on the type and shape of the polygon. For regular polygons, the area is usually calculated using specialized formulas.

4. Measuring Angles in Polygons

• To calculate the sum of the interior angles of a polygon, you can use the formula (n - 2) × 180°, where n is the number of sides. This formula helps in determining the shape of the polygon and is essential for problem-solving in geometry.
• Exterior angles of a polygon (created by extending one side of each angle) will always sum to 360 degrees regardless of the number of sides.

5. Naming Polygons

• Knowing the names of polygons based on the number of sides can simplify communication about these shapes. From triangles (3 sides) and quadrilaterals (4 sides) to dodecagons (12 sides) and beyond, each has a specific name.

6. Practical Applications of Polygons

• Polygons appear in many aspects of daily life and in various fields. Engineers and architects use polygons in designing buildings, roads, and bridges. Artisans and designers incorporate them into patterns and jewelleries.
• In technology, polygons are crucial in computer graphics and simulations. They are used to build 3D models and environments in video games and virtual reality, creating visually compelling digital worlds.

7. Polygons in Nature and Art

• Nature often inspires the use of polygons: honeycombs in beehives are hexagonal; the sections of a turtle's shell form a polygonal pattern. These shapes not only provide strength and efficiency in nature's designs but also inspire human applications in architecture and art.
• In art, polygons are used to create abstract and geometric art, where artists play with the shapes, sizes, and colors of polygons to produce intriguing designs.

8. Advanced Polygons

• For those looking to deepen their understanding of geometry, exploring polygons further can involve studying higher mathematics topics like topology, symmetry in polygons, and tiling patterns, which have applications in scientific fields.

Conclusion

Polygons are more than just basic shapes; they are a fundamental part of geometry that link to many other aspects of mathematics and real-world applications. From simple triangles to complex polygons, the diversity and utility of polygons make them an essential area of study in both academic learning and practical applications. Understanding the various types and properties of polygons not only enriches one’s geometrical knowledge but also enhances problem-solving and critical thinking skills used in daily life and various professional fields.