Introduction to Quadratic Equation

A quadratic equation is a polynomial equation of a second degree of the form: ax2+bx+c=0, where x represents the variable and a, b and c are constants with a≠0.

The solutions to a quadratic equation can be found using the quadratic formula:

x = [-b±√(b2-4ac)]/2a

The expression b2 – 4ac is called the discriminant. The discriminant of a quadratic equation is a mathematical expression derived from the coefficients of the quadratic equation. It is used to determine the nature of the roots of the quadratic equation without explicitly solving for them. 

If D > 0, the quadratic equation has two different real roots which are distinct and real numbers

If D = 0, the quadratic equation has two real roots that are equal

If D < 0, the quadratic equation has two complex roots.

Example 1: Solve the equation x2-5x+6

In the above equation a=1, b=-5 and c=6

discriminant D= b2-4ac = 25-24=1

As D>0,the roots of the equation are real and unequal

x1=(5 + √1)/2=3

x2=(5- √1)/2=2

Hence the roots of the quadratic equation are 3 and 2

The sum and product of the roots of a quadratic equation

for the quadratic equation ax2+bx+c=0 

Sum of the roots = -b/a

Products of the roots = c/a

The graph of a quadratic equation is a Parabola.

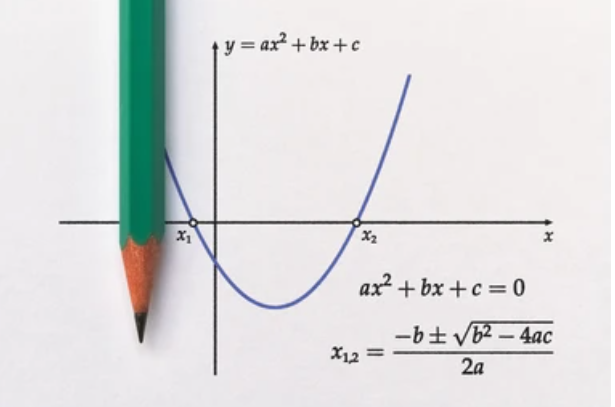
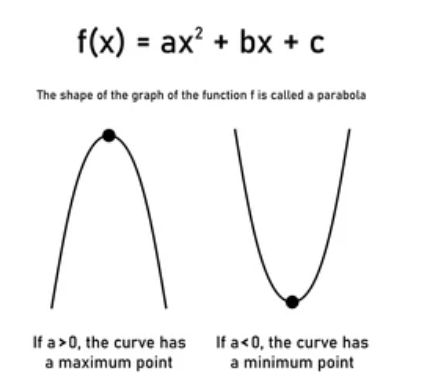
When the coefficient of  x2 is positive the parabola opens upwards and it open downward when the coefficient of x2 is negative. 

For the standard quadratic equation  y= ax2+bx+c the vertex of the parabola can be found using the formula x = -b/2a and substituting it back into the standard equation we get y= - D/4a, hence vertex is (-b/2a,-D/4a), where D =b2-4ac.

The axis of symmetry of a parabola is a vertical line that divides the parabola into two equal halves. It passes through the vertex of the parabola. For parabola in the standard form y= ax2+bx+c , the axis of symmetry is given by x =  -b/2a