Static and Kinetic Friction
Static and Kinetic Friction
Friction is a force that resists the relative motion between two surfaces in contact. Static and kinetic friction are its two primary types, defined based on the state of motion of the objects:
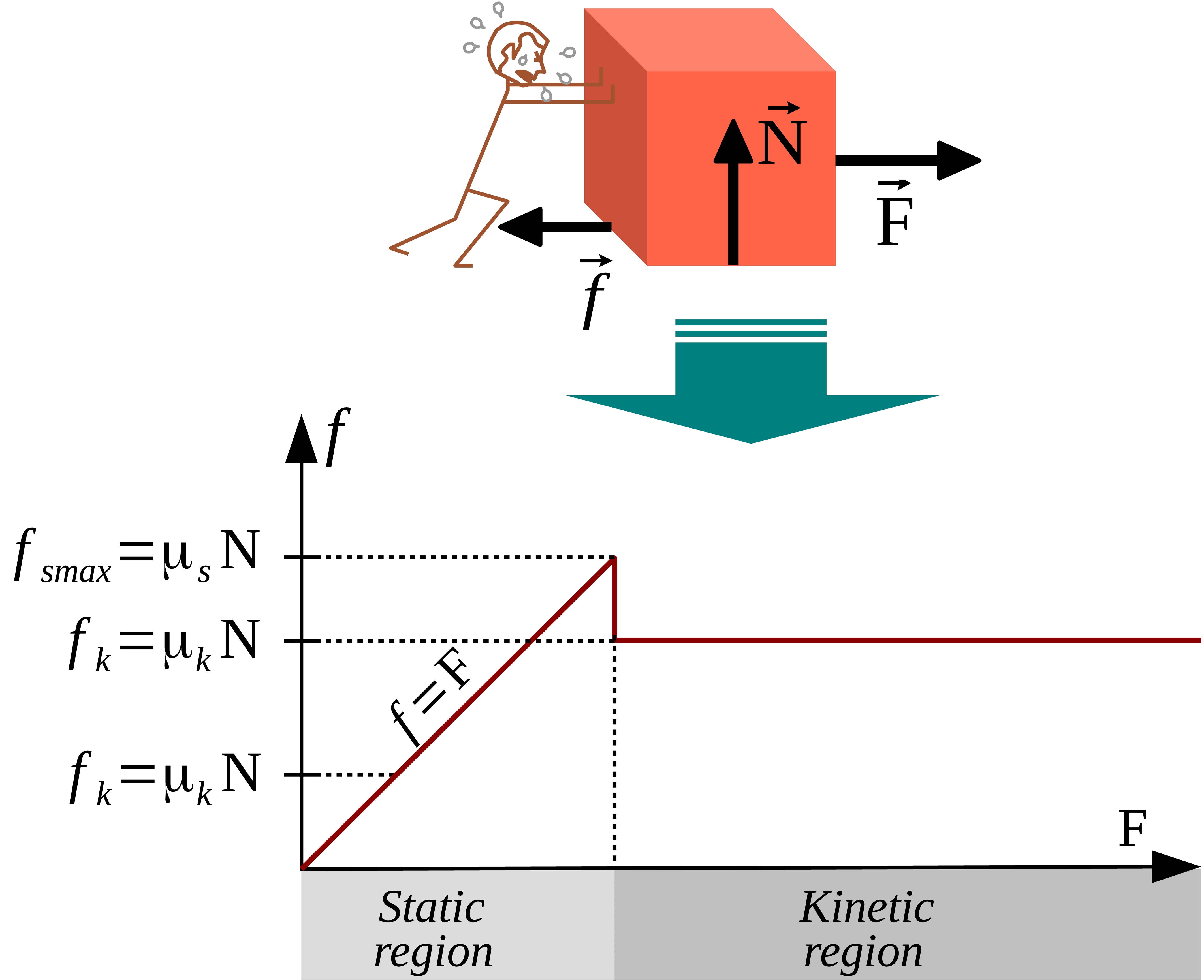
1. Static Friction
- Definition: The frictional force that prevents an object from starting to move when a force is applied.
- Key Characteristics:
- Acts when there is no relative motion between the surfaces (the object is at rest).
- Increases with the applied force until it reaches a maximum value, beyond which the object starts to move.
- It is greater than kinetic friction for most materials.
- Formula: fs≤μsN Where:
- fs: Static frictional force
- μs : Coefficient of static friction (depends on the surfaces in contact)
- N: Normal force (perpendicular force exerted by the surface)
2. Kinetic (Dynamic) Friction
- Definition: The frictional force that resists the motion of an object already in motion.
- Key Characteristics:
- Acts when there is relative motion between the surfaces (sliding motion).
- It remains constant for a given pair of surfaces and is independent of the relative speed.
- Generally less than the maximum static friction.
- Formula: fk=μkN Where:
- fk : Kinetic frictional force
- μk : Coefficient of kinetic friction
- N: Normal force
Comparison of Static and Kinetic Friction
| Aspect | Static Friction | Kinetic Friction |
| State of Motion | Prevent motion (Object is at rest) | Resist motion (Object is moving) |
| Magnitude | Varies up to a maximum value | Constant for a given pair of surfaces |
| Formula | fs≤μsN | fk=μkN |
| Coefficient | μs (usually larger). | μk (usually smaller). |
Examples
- Static Friction:
A heavy box on a rough floor doesn’t move even when you push it lightly because the static friction opposes your force. - Kinetic Friction:
Once the box starts sliding, a constant force is required to maintain its motion because kinetic friction opposes the sliding.
Applications
- Static Friction: Preventing slipping (e.g., between car tires and roads, or objects on a sloped surface).
- Kinetic Friction: Understanding wear and energy losses in moving parts (e.g., in machines or vehicles).
Understanding these two forces is crucial for designing machines, predicting motion, and solving various physics problems.
Here are some examples of numericals involving static and kinetic friction:
Example 1: Maximum Static Friction
A block of mass 10 kg is resting on a horizontal surface. The coefficient of static friction (μs) between the block and the surface is 0.40. What is the maximum force that can be applied before the block starts moving?
Solution:
- Given:
- Mass of the block, m=10 kg
- Coefficient of static friction, μs=0.4
- Acceleration due to gravity, g=9.8 m/s2
- Calculate Normal Force: N=m⋅g=10⋅9.8=98 N
- Calculate Maximum Static Friction: fs=μs⋅N=0.4⋅98=39.2
- Answer: The maximum force that can be applied is 39.2 N
Example 2: Kinetic Friction Force
A 5 kg block is sliding on a rough surface with a coefficient of kinetic friction (μk) of 0.30 . Find the force of kinetic friction acting on the block.
Solution:
- Given:
- Mass of the block, m=5 kg
- Coefficient of kinetic friction, μk=0.3
- Acceleration due to gravity, g=9.8 m/s2
- Calculate Normal Force: N=m⋅g=5⋅9.8=49 N
- Calculate Kinetic Friction: fk=μk⋅N=0.3⋅49=14.7 N Answer: The force of kinetic friction is 14.7 N
Example 3: Object in Motion with Applied Force
A horizontal force of 50 N is applied to a 20 kg block resting on a surface with μs=0.5 and μk=0.3. Will the block move? If yes, what will be its acceleration?
Solution:
- Given:
- Mass of the block, m=20 kg
- Applied force, F=50 N
- μs=0.5 , μk=0.3
- g=9.8 m/s2
- Calculate Normal Force: N=m⋅g=20⋅9.8=196 N
- Calculate Maximum Static Friction: fs=μs⋅N=0.5⋅196=98
- Compare Applied Force with Maximum Static Friction: Since the applied force (50 N) is less than fs=98 N, the block will not move.
Answer: The block will not move because the applied force is less than the maximum static friction.
Example 4: Acceleration of a Moving Object
If the force applied in the above problem is increased to 120 N, what will be the acceleration of the block?
Solution:
- Compare Applied Force with Maximum Static Friction: Since 120 N>98 N the block will move.
- Calculate Kinetic Friction: fk=μk⋅N=0.3⋅196=58.8 N
- Net Force Acting on the Block: Fnet=F−fk=120−58.8=61.2 N
- Calculate Acceleration: a =Fnet/m =61.2/20 =3.06 m/s2
Answer: The acceleration of the block is 3.06 m/s2.